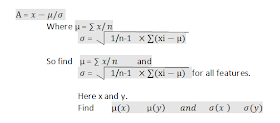How To Workout SVM Algorithm
In machine learning, support vector machines (SVMs, also support vector networks) are supervised
learning models
with associated learning algorithms that analyze data and
recognize patterns, used for classification and regression
analysis. The basic SVM takes a set of input data and predicts,
for each given input, which of two possible classes forms the output, making it
a non-probabilistic binary linear classifier.
Given a set of training examples, each marked as belonging to one of two
categories, an SVM training algorithm builds a model that assigns new examples
into one category or the other. An SVM model is a representation of the examples
as points in space, mapped so that the examples of the separate categories are
divided by a clear gap that is as wide as possible. New examples are then
mapped into that same space and predicted to belong to a category based on
which side of the gap they fall on.
More formally, a support vector machine constructs a hyper plane or set of hyper planes in a high- or
infinite-dimensional space, which can be used for classification, regression,
or other tasks. Intuitively, a good separation is achieved by the hyper plane that has the largest distance to the nearest training data point of any class
(so-called functional margin), since in general the larger the margin the lower
the generalization
error of
the classifier.
1.1 SVM Binary Classification Algorithm
Example 1:
Step 1:Normalize the given data by
using the equation
Step 2: Compute Augmented matrix [A
-e]. ie Augment a "-1" column matrix to A.
Step 3: Compute H = D[A -e]
Step 4 : Compute U = V ×[I –H[I/V + HTH]-1 HT]×e
Where I = Identity Matrix
V = Order of HTH with value 0.1
Step 5: Find w and gamma = 0.

Step 6: Find w trans * X -gamma. Find for all features
eg: X= Column_matrix{x,y}
Step 7: Compare sign(wT*x -gama ) with the actual class label.
You can notice that 3rd , 5 th and 9 th class labels are misclassified.
ie
After Traning the dataset , the below datapoints
5 9 falls in class label -1
8 7 falls in class label -1
and
8 5 falls in class label 1.
Misclassification in 3 datapoints 3 rd 5 th and 9 th.
Acurracy is 70%.